「ポートフォリオを形成することで、リスクが低減できる 」
株式投資をしていて、こんな話を聞いたことがないでしょうか。
ポートフォリオとは、さまざまな資産を組み合わせて、リスクを低減して、リターンを最大化するような資産構成のことをいいます。
しかし、多くの人はポートフォリオを組むとなぜリスク低減できるか説明せよと言われると、難しいのではないでしょうか。
ファイナンス理論では、互いに連動性のない資産でポートフォリオを組むと個別株式リスクが軽減されると言われています。
この記事では、このポートフォリオを組むことによるリスク軽減を定量的に表現しながら解説していきます。
単一銘柄に投資をした場合のリスク
投資家が、次のような電力株に投資したと仮定します。
■電力株のリターン
| 事象 | 確率 | リターン |
| 円高 | 40% | 5% |
| 横這い | 20% | 3% |
| 円安 | 40% | 1% |
この電力株は、為替の影響は受けにくいのですが、円高になると外国人投資家が通貨価値上昇を狙って投資をしてくると仮定します。
このときの、投資家のリスクを計算します。
リスクの計算のために、まずリターンの期待値Eを求めます。
E = 0.4×5% + 0.2×3% + 0.4×1%
= 3.0%
このときリスクは、リターンの標準偏差σで表すことができます。
σ2 = 0.4×(5.0%-3.0%)2 + 0.2×(3.0%-3.0%)2 + 0.4×(1.0%-3.0%)2
σ = 1.79%
組み合わせたい銘柄のリスク
次に、投資家が、次のような自動車株をポートフォリオに入れたいと考えたとします。
■自動車株のリターン
| 事象 | 確率 | リターン |
| 円高 | 40% | -2% |
| 横這い | 20% | 4% |
| 円安 | 40% | 8% |
為替が円高になれば、輸出商品の収益が小さくなり、リターンはマイナスとなると仮定します。一方、為替が横這いの場合は、企業の成長分だけリターンが得られ、円安の場合は、輸出商品の収益アップによりリターンが大きくなると仮定します。
このときの、自動車株単体でのリターンの期待値Eとリスクσを求めます。
E = 0.4×-2% + 0.2×4% + 0.4×8% = 3.2%
σ2 = 0.4×(-2.0%-3.2%)2 + 0.2×(4.0%-3.2%)2 + 0.4×(8.0%-3.2%)2
σ = 4.49%
ポートフォリオを作ったときのリスク
では、2.つの銘柄を組み合わせたときのリスクを見てみます。ここでは、電力株を60%、自動車株を40%の割合でもつと仮定します。
まず、円高、横這い、円安の各局面でのリターンを計算します。
円高 5%×0.6 + -2%×0.4 = 2.0%
横這い 3%×0.6 + 4%×0.4 = 3.4%
円安 1%×0.6 + 8%×0.4 = 3.8%
したがって、ポートフォリオ作成時のリターンは下の表のようになります。
■ポートフォリオ作成時のリターン
| 事象 | 確率 | リターン |
| 円高 | 40% | 2.0% |
| 横這い | 20% | 3.4% |
| 円安 | 40% | 3.8% |
ここで、同じように期待値Eとリスクσを計算すると次のようになります。
E = 0.4×2.0% + 0.2×3.4% + 0.4×3.8% = 3.08%
σ2 = 0.4×(2.0%-3.0%)2 + 0.2×(3.4%-3.0%)2 + 0.4×(3.8%-3.0%)2
σ = 0.73%
この計算から、異なる動きをする銘柄でポートフォリオを組むとリスクが軽減されるということがわかります。ここで特筆すべきなのは、リスクの低い電力株だけのときより、よりリスクの高い自動車株を組み合わせたときの方がリスクが小さくなるという点です。
ポートフォリオ作成時のリスク・リターンの関係
上のケースでは、電力株と自動車株を6:4の組み合わせにすることで、リスクを減らせることを説明しました。ここで、銘柄比率を変化させたとき場合にどうなるか考えてみます。
上のケースにおける、リスクと期待リターンの関係を次のようにグラフにします。
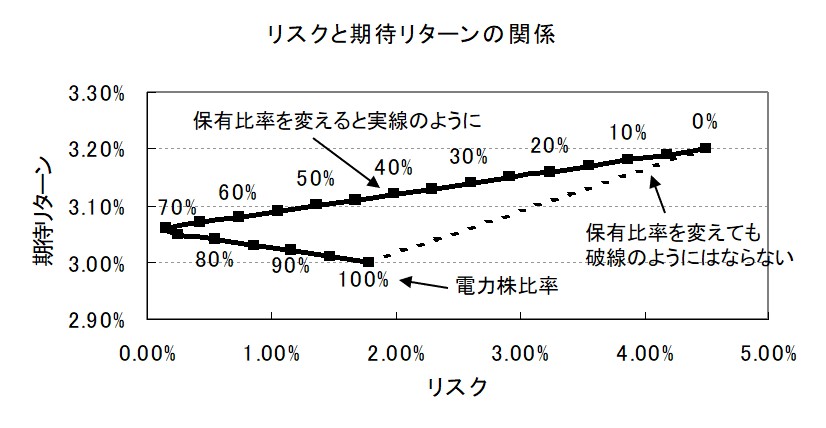
このグラフから、同じリスクでも期待リターンの異なる場合があるということがわかります。つまり、投資家は、ポートフォリオをうまく組んで、単体保有のときと同じリスクで、期待リターンを大きくすることが可能なわけです。
相関係数とリスク・リターンの関係
互いに連動しない、2つの銘柄でポートフォリオを組むと、最適なリスクとリターンになるような比率が存在することがわかりました。実は、このリスクとリターンは、2つの銘柄の相関係数と密接な関係があります。

相関係数が-1の場合、リスクがゼロになる点が存在し、相関係数が1の場合は、2銘柄が全く同じように動くので、リスクとリターンの関係は直線で表現できます。
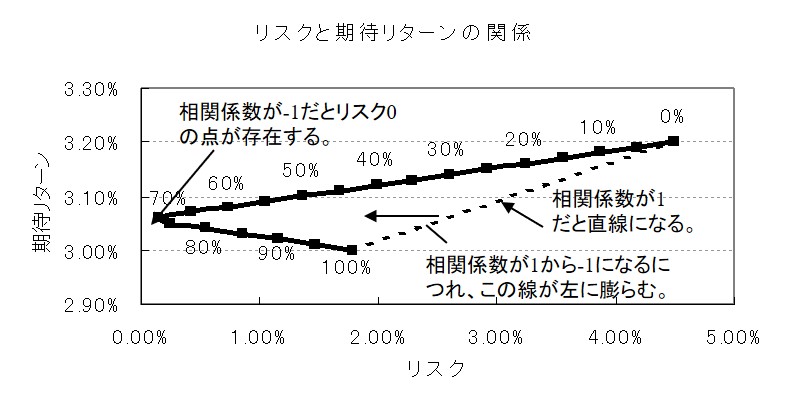
実際は、2銘柄の相関係数が-1や1になることはありませんが、2銘柄の相関によってリスクとリターンの関係がどうなるのかを把握しておくことは重要です。2銘柄の相関係数は過去の株価変動から算出することができます。
効率的フロンティア
上の例では、2つの銘柄でポートフォリオを組んだ場合を示しましたが、無数のポートフォリオを組んだ場合のリスクとリターンの関係は次のようになります。
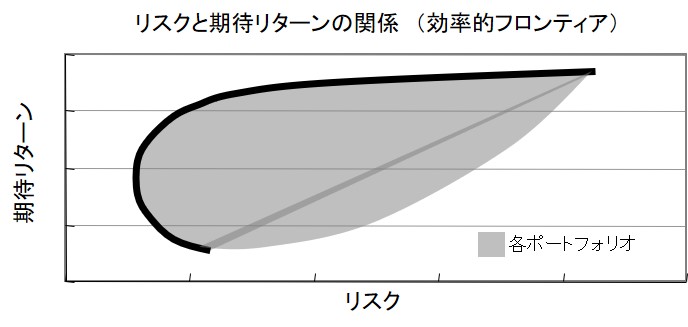
グレーの部分は、株式の組み合わせによって無数に存在するポートフォリオです。投資家は、できる限りリスクを極小化して、リターンを極大化しようとするため、結果的にグラフ上の太線のポートフォリオを選択することになります。これを効率的フロンティア(エフィシェント・フロンティア)と呼びます。
実際の株式銘柄間で相関係数を求めてみる
ポートフォリオを組んだときのリスク分散は、銘柄間の相関係数によって決まることを説明しましたが、実在する銘柄間での相関係数の求め方を解説します。(少々古い例にはなりますが、考え方の理解の妨げにはならないので、ご容赦ください)
過去の株価情報を拾う
過去の株価情報はヤフーファイナンスの時系列データで確認することができます。ここでは、2003年1月~2006年12月まで1ヶ月ごとの株価情報から相関係数を求めます。(株価は、分割などの影響を排除した調整後終値を使用します。
| 日産自動車 | トヨタ自動車 | 日産自動車 | トヨタ自動車 | |
| 日付 | 調整後終値* | 調整後終値* | 前月との 終値の差 |
前月との 終値の差 |
| 2006年12月 | 1,433 | 7,960 | 21 | 940 |
| 2006年11月 | 1,412 | 7,020 | 11 | 90 |
| 2006年10月 | 1,401 | 6,930 | 78 | 510 |
| 2006年9月 | 1,323 | 6,420 | -11 | 50 |
| 2006年8月 | 1,334 | 6,370 | 98 | 310 |
| 2006年7月 | 1,236 | 6,060 | -14 | 70 |
| 2006年6月 | 1,250 | 5,990 | -100 | 60 |
| 2006年5月 | 1,350 | 5,930 | -147 | -730 |
| 2006年4月 | 1,497 | 6,660 | 99 | 230 |
| 2006年3月 | 1,398 | 6,430 | 58 | 180 |
| 2006年2月 | 1,340 | 6,250 | 20 | 170 |
| 2006年1月 | 1,320 | 6,080 | 125 | -40 |
| 2005年12月 | 1,195 | 6,120 | -38 | 330 |
| 2005年11月 | 1,233 | 5,790 | 25 | 480 |
| 2005年10月 | 1,208 | 5,310 | -88 | 110 |
| 2005年9月 | 1,296 | 5,200 | 140 | 700 |
| 2005年8月 | 1,156 | 4,500 | -12 | 250 |
| 2005年7月 | 1,168 | 4,250 | 70 | 280 |
| 2005年6月 | 1,098 | 3,970 | 31 | 110 |
| 2005年5月 | 1,067 | 3,860 | 27 | 20 |
| 2005年4月 | 1,040 | 3,840 | -59 | -150 |
| 2005年3月 | 1,099 | 3,990 | -26 | -80 |
| 2005年2月 | 1,125 | 4,070 | 30 | 40 |
| 2005年1月 | 1,095 | 4,030 | -19 | -140 |
| 2004年12月 | 1,114 | 4,170 | 29 | 310 |
| 2004年11月 | 1,085 | 3,860 | -110 | -270 |
| 2004年10月 | 1,195 | 4,130 | -5 | -90 |
| 2004年9月 | 1,200 | 4,220 | 8 | -100 |
| 2004年8月 | 1,192 | 4,320 | -10 | -160 |
| 2004年7月 | 1,202 | 4,480 | -11 | 60 |
| 2004年6月 | 1,213 | 4,420 | 100 | 420 |
| 2004年5月 | 1,113 | 4,000 | -116 | 10 |
| 2004年4月 | 1,229 | 3,990 | 64 | 110 |
| 2004年3月 | 1,165 | 3,880 | -48 | 110 |
| 2004年2月 | 1,213 | 3,770 | 84 | 310 |
| 2004年1月 | 1,129 | 3,460 | -95 | -160 |
| 2003年12月 | 1,224 | 3,620 | -28 | 330 |
| 2003年11月 | 1,252 | 3,290 | 20 | 160 |
| 2003年10月 | 1,232 | 3,130 | 27 | -150 |
| 2003年9月 | 1,205 | 3,280 | -48 | 60 |
| 2003年8月 | 1,253 | 3,220 | 78 | 170 |
| 2003年7月 | 1,175 | 3,050 | 27 | -60 |
| 2003年6月 | 1,148 | 3,110 | 205 | 250 |
| 2003年5月 | 943 | 2,860 | 28 | 160 |
| 2003年4月 | 915 | 2,700 | 125 | 65 |
| 2003年3月 | 790 | 2,635 | -97 | -140 |
| 2003年2月 | 887 | 2,775 | -26 | -80 |
| 2003年1月 | 913 | 2,855 |
相関係数を求める
抽出した株価情報を元に、各月の株価の変動を求めます。そして2銘柄の株価変動に対して相関係数を求めます。(エクセルを使う場合は、CORREL関数で相関係数を求められます。)
日産とトヨタの場合、相関係数は0.54になります。
一般的に0.7以上ないと相関があるとはいえないので、日産とトヨタの場合あまり相関があるとはいえないようです。おそらく同じ自動車メーカーでもビジネスの仕組みが異なり、外部要因に対する変動の仕方が異なるためでしょう。
同業種・異業種での相関係数
日産とトヨタの例では相関係数があまり高くなかったのですが、一般的に、同業種同士は株価変動の相関係数は高く、異業種同士の株価変動の相関係数は低くなることが想定できます。
同じアパレル業界のポイントとユナイテッドアローズで求めてみたところ、相関係数は0.74となり、日産とトヨタの場合に比べて相関係数が高く、絶対値で見ても相関があるといえる関係になっています。
では、トヨタとユナイテッドアローズで見るとどうなるでしょうか?計算してみると相関係数は0.34となり、かなり相関が低いことがわかりました。
円安で利益がプラスになりやすいトヨタと、逆に円高で利益がプラスになりやすいユナイテッドアローズのビジネスシステムの違いが、相関係数が低くなる一因と考えられます。
財務・ファイナンスをもっと知るには


