相関係数とは？【意味・目安・エクセルでの求め方】

相関係数とは、2つの変数の相関関係を数値で示したものです。

相関係数を使うことで、特定の2つの変数の関係性（たとえば身長と体重の関係性）の強さを判断できるようになります。

相関係数は必ず-1～1の範囲に収まるようになっていて、その値によって「正の相関がある」「負の相関がある」「相関なし」などと判断できます。

このように、相関係数を用いて相関関係を分析することを相関分析と呼びます。

この記事では、相関係数の目安や計算方法、注意点について解説していきます。

物事の相関関係・因果関係を明らかにする能力を高めることは、ロジカルシンキングの能力を鍛えることにもつながります。

相関係数の計算方法

変数xと変数yの相関係数は、「xとyの共分散」を「xの標準偏差とyの標準偏差の積」で割ることで計算できます。

一見すると複雑な計算式に見えてしまいます。

しかし、計算式によって相関係数を求めることはレアで、実務上はエクセルなどの表計算ソフトを使って一瞬で求めるの一般的です。

エクセルを使った相関係数の求め方は後ほど解説します。

相関係数とグラフの例

相関係数をグラフを使って視覚的に見てみましょう。

2つの変数の一方を横軸、他方を縦軸にとることで、相関関係の有無を視覚的に判断できます。

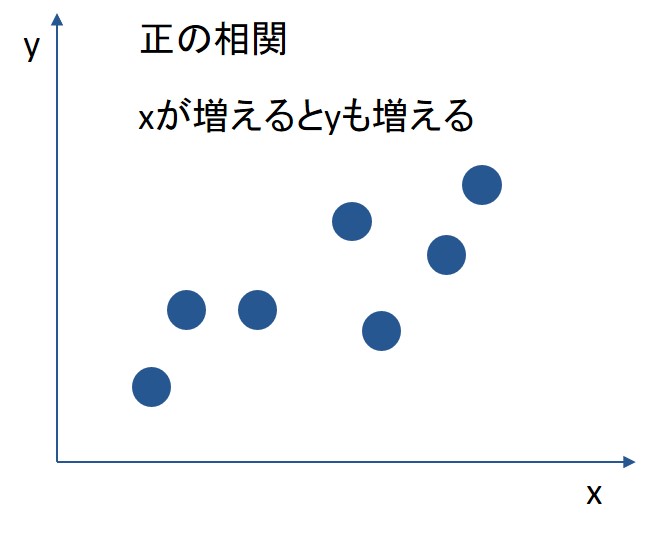
正の相関とグラフ例

相関係数が1に近づくほど、正の相関（片方の値が上がれば、もう片方の値が一定の割合で上がる関係）があると言え、相関係数が1のときは、完全な正の相関があることになります。

以下のグラフは、xとyに正の相関がある場合の代表例です。

負の相関とグラフ例

相関係数が-1に近づくほど、負の相関（片方の値が上がれば、もう片方の値が一定の割合で下がる関係）があると言え、相関係数が-1だと完全な負の相関があることになります。

以下のグラフは、xとyに負の相関がある場合の代表例です。

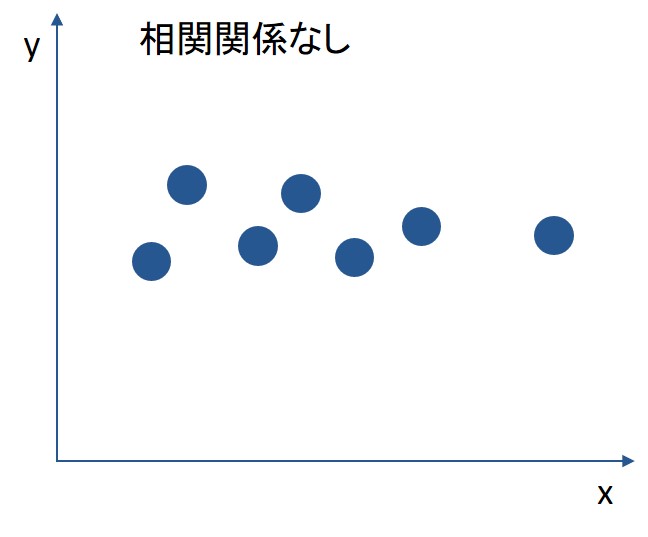
相関なしとグラフ例

相関係数の絶対値が0に近づくと、相関関係がないと判断でき、相関駅数が0のときは、全く相関関係がないことになります。

以下のグラフは、xとyに相関関係がない場合の代表例です。

相関係数の目安（相関の強い・弱いの目安）

相関係数の目安として、一般的に相関係数の絶対値が0から0.2の間では相関関係なし、0.2～0.4では弱い相関関係あり、0.4から0.7では相関関係あり、0.7以上だと強い相関関係があると考えられています。

相関係数と相関関係の目安を、表で示すと以下のとおりになります。

相関係数（r）	相関関係
0.7 ≦ r	強い正の相関関係
0.4 ≦ r ≦ 0.7	正の相関関係
0.2 ≦ r ≦ 0.4	弱い正の相関関係
-0.2 ≦ r ≦ 0.2	相関関係なし
-0.4 ≦ r ≦ -0.2	弱い負の相関関係
-0.7 ≦ r ≦ -0.4	負の相関関係
r ≦ -0.7	強い負の相関関係

相関係数とR²値の違い

相関係数と似た値にR²値があります。

相関係数とR²値は、両方とも2つの変数の関係性を示す指標ですが、異なるものです。

相関係数は、2つの変数の間の線形関係の強さを表す値で、-1から1の範囲で表されます。

したがって相関係数には、上記のとおり正の相関と負の相関があります。

一方でR²値は、1つの変数がもう1つの変数の変動によってどれだけを説明できるかを示す指標で、0から1の範囲で表されます。

両方とも、2つの変数の関係性を示す指標ではあるものの、異なる観点から評価しているのです。

ただし相関係数とR²値には密接関係性があり、R²値相関係数の2乗によって求められるのです。（回帰分析をもっと知りたい方は⇒　回帰分析の詳細）

相関係数をエクセル求める方法

相関係数はエクセルのCORREL関数を用いれば、簡単に求めることができます。

たとえば、次のような1と2についての相関関係を求めてみます。

1	10	12	3	14	4	10	6	11	9	11
2	16	17	3	26	7	18	10	15	15	14

これらの値をエクセルに以下のように貼り付けて、CORREL関数を使うことで、簡単に相関係数を求めることができます。

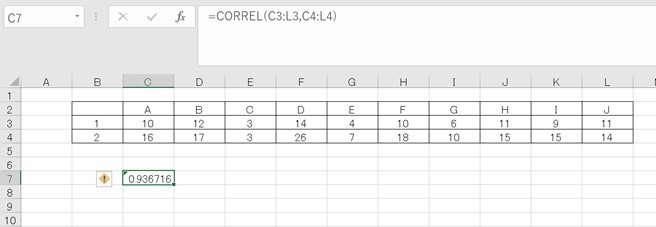
この例の場合、相関係数は約0.937となり、かなり相関が強いことがわかります。

相関係数を用いる際の注意点

相関係数を用いる際に注意すべき点が3つあります。

それぞれ詳細を見ていきましょう。

相関があるからといって因果関係があるわけではない

相関係数から強い相関が発見できても、それらに因果関係があるとまでは言い切れないません。

たとえば、年収に対する糖尿病患者の割合に相関があったとしても、2者には直接的な因果はなく、それは第3の因子である食生活との因果関係である可能性があります。

ある事象同士の相関関係が見られたときには、その2つに本当に因果関係があるのかを注意深く見ていく必要があります。

相関から外れた値の扱いに注意する

2つの値の関係をグラフにすると、明らかに外れたデータが出てくる場合があります。

こうしたデータを含んだまま、相関係数を出すと、相関関係が弱いがという結果が出てしまいます。

もし、相関から外れた値が、特定の条件で発生したものであれば、外れた値を一旦取り除いて相関係数を計算しなおす必要があります。

また、こうしたデータにはビジネス上の大きなヒントが隠されている場合もあるので、注意して掘り下げてみることも必要です。

相関の判断はビジネスの種類によって違う

相関があると言うためには、一般的に相関係数が＋0.7以上または-0.7以下（R²値だと0.5くらい）は必要ですが、ビジネスの性質によってはそれ以下でも相関関係を深堀して考える場合があります。

たとえば、医薬品の副作用のように、万が一相関があった場合のリスクが極めて大きい場合などは、相関係数が低くてもしっかり内容を調査する必要があります。

ビジネスでの相関係数の事例

相関係数のビジネスへの応用事例の1つとして、ファイナンスのポートフォリオ理論があります。

ポートフォリオ理論とは、全てのお金を1つの銘柄に集中させるのではなく、互いに相関関係の弱い銘柄に分散させて保有することで、一定のリターンが期待できながらも、リスクを大きく抑えられるという理論です。

ポートフォリオ理論の詳細は、以下の記事で解説しています。

ポートフォリオを組むとリスクを分散できる理由【理論を解説】「ポートフォリオを形成することで、リスクが低減できる 」 株式投資をしていて、こんな話を聞いたことがないでしょうか。 ポート...

まとめ

以上、相関係数の解説でした。