弱者の戦略として有名な経営戦略のフレームワークにランチェスター戦略があります。
ランチェスター戦略を知ることで、戦略的に劣る弱者が、戦力的に勝る強者とどのように戦えばよいか示唆を得ることができます。
この記事では、ランチャスター戦略の元になっている考え方を踏まえて、図解を交えながらランチャスター戦略について解説していきます。
ランチャスター戦略とは
ランチェスター戦略とは、イギリスのフレデリック・W・ランチェスターによって、第一次世界大戦における航空機による空中戦の損害状況を研究から生み出されたものです。
ランチェスターは、戦闘をする双方が同じ武器を持っているとするなら、勝敗は兵力数によって決まることを示し、その法則はランチェスターの法則と呼ばれています。
このランチェスターが見つけた法則は、さらに2つに分類されます。
ランチェスターの第一法則
1つは、ランチェスターの第一法則です。
ランチェスターの第一法則とは、互いの兵士が一騎打ちすることを前提にした法則です。
たとえば、A国の兵士100人とB国の兵士50人が一騎打ちをすると、双方が同じ損害を受けて最終的にA国の兵士50人が生き残ります。
第一法則では、戦闘力を次のように定義できます。
戦闘力 = 武器性能 × 兵力数
もし互いの武器性能が同じであれば、この式は次のように書き換えることもできます。
(戦闘前のA国の兵力数) ー (戦闘前のB国の兵力数)
= (戦闘後のA国の兵力数)
A国の兵力数 > B国の兵力数の場合
つまり、兵力数の差は常に一定であると言い換えることもできます。
実際にA国とB国の兵力数が以下のようになっているとします。
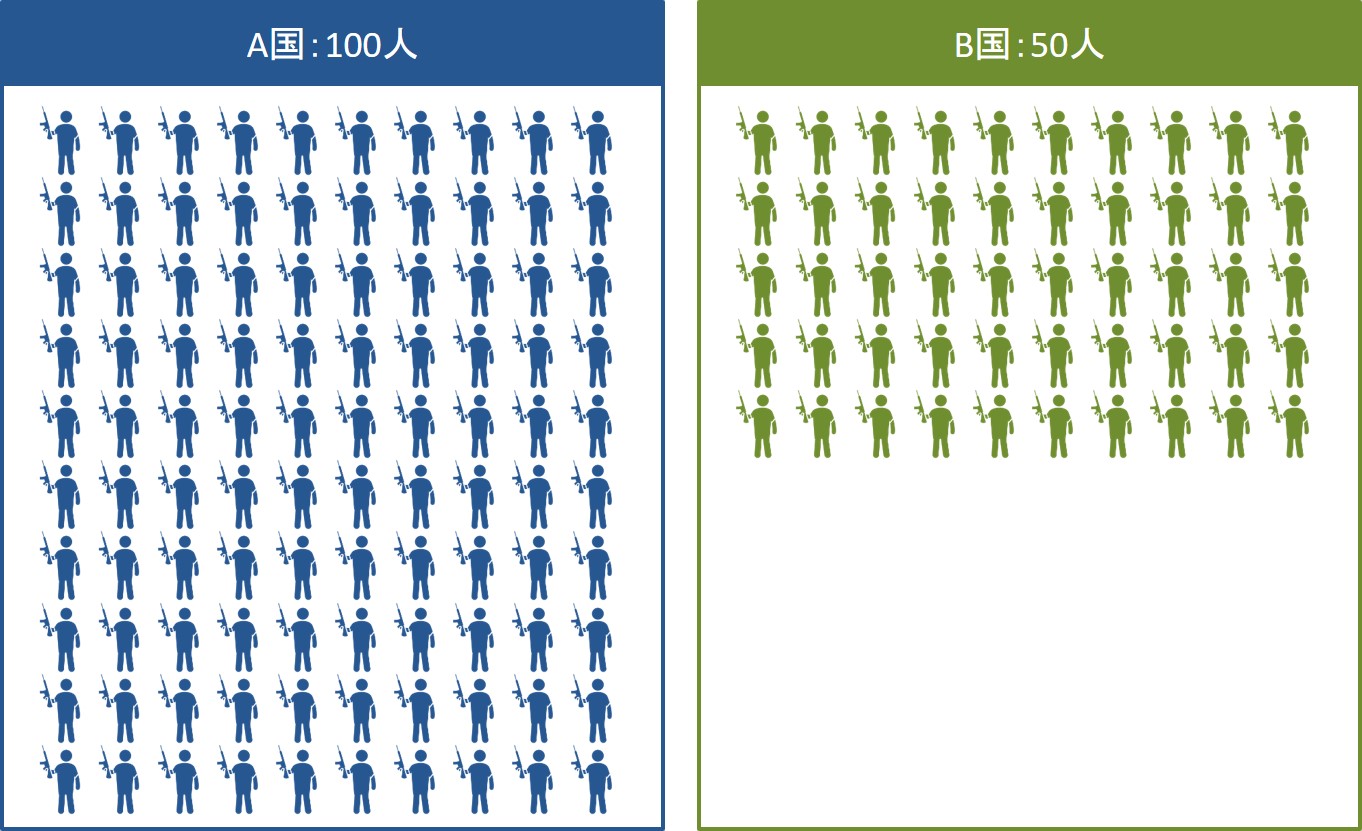
ランチェスターの第一法則によると、戦闘後の兵力数は次のようになります。

ランチェスターの第二法則
もう1つは、ランチェスターの第二法則です。
ランチェスターの第二法則とは、第一法則の前提よりもより広域な遠隔戦・集団戦を前提にした法則です。
たとえば、A国の兵士100人とB国の兵士50人が遠隔戦をすると、最終的にA国の兵士86人が生き残るとされています。
これは、第二法則では、以下のように戦闘力を兵力数の2乗に比例すると考えるからです。
戦闘力 = 武器性能 × (兵力数)^2
もし互いの武器性能が同じであれば、この式は次のように書き換えることもできます。
(戦闘前のA国の兵力数)^2 ー (戦闘前のB国の兵力数)^2
= (戦闘後のA国の兵力数)^2
A国の兵力数 > B国の兵力数の場合
つまり、兵力数の2乗の差は常に一定であると言い換えることもできます。
ランチェスターの第二法則を活用すると、先ほどのA国100人、B国50人の兵力数は戦闘後に以下のようになります。

ランチェスター戦略を活用した弱者の戦略
ランチェスターの法則から示唆される弱者の戦略は以下の2つです。
- 局地戦に持ち込む
- 一点突破をする
- 相手を分断する
局地戦に持ち込む
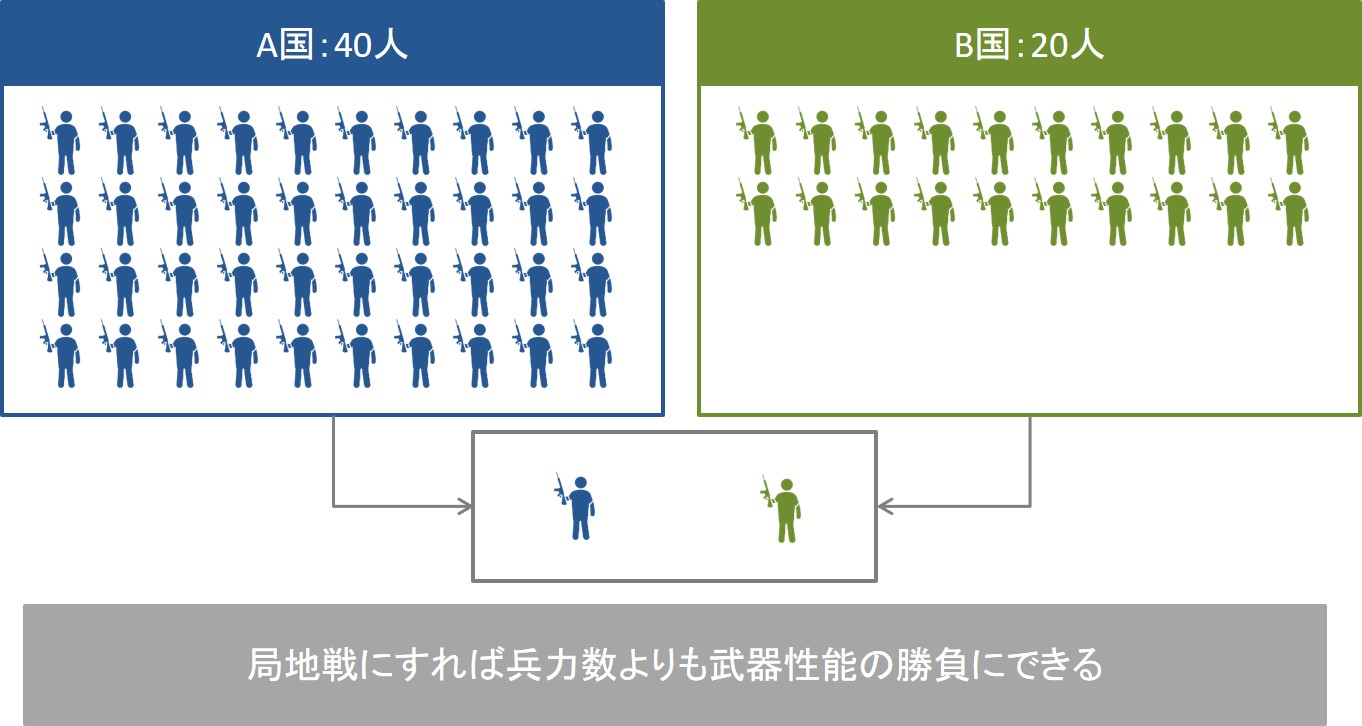
ランチェスターの第一法則によると、局地戦で一騎打ちに持ち込めば兵力数の差に比べて質の方が相対的に重要であることがわかります。
したがって、相手が自分たちの2倍の大きさを誇る相手であっても、1対1で戦える状態を作っていけば、質で相手を打ち負かせる可能性が出てくるのです。
このように、局地戦にして相手が集団で戦えないようにすることが、弱者の戦略の1つになります。
一点突破をする
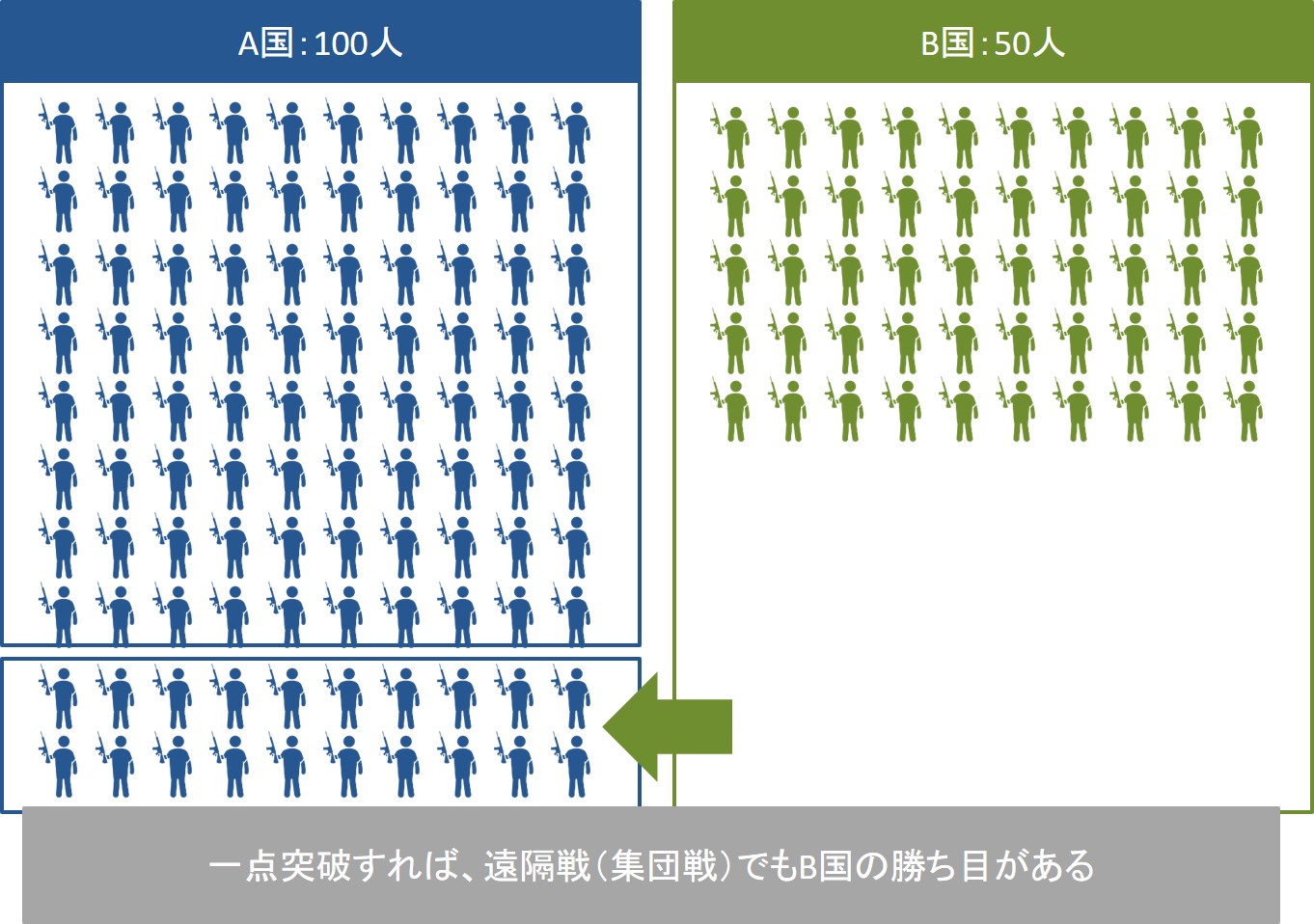
ランチェスターの第二法則によると、物量に劣る弱者が、物量に勝る強者に対して集団戦を仕掛ければ惨敗することは先ほど示したとおりですが、同じ集団戦であっても一点突破を図る前提にすれば勝ち目が出てきます。
先ほどの例だと、兵力数が100人のA国に対して、20人しかいないところを見つけて、そこにB国が50人で集団戦を仕掛ければ、B国が圧勝することができます。
相手を分断する
弱者が強者に集団戦の全面戦争を仕掛けても惨敗するのは、先ほど書いたとおりですが、もし相手を分断することができれば、個別に撃破することで弱者が強者に勝ることも可能です。
先ほどの例だと、A国の兵力数100人を20人ずつに分断できたとします。
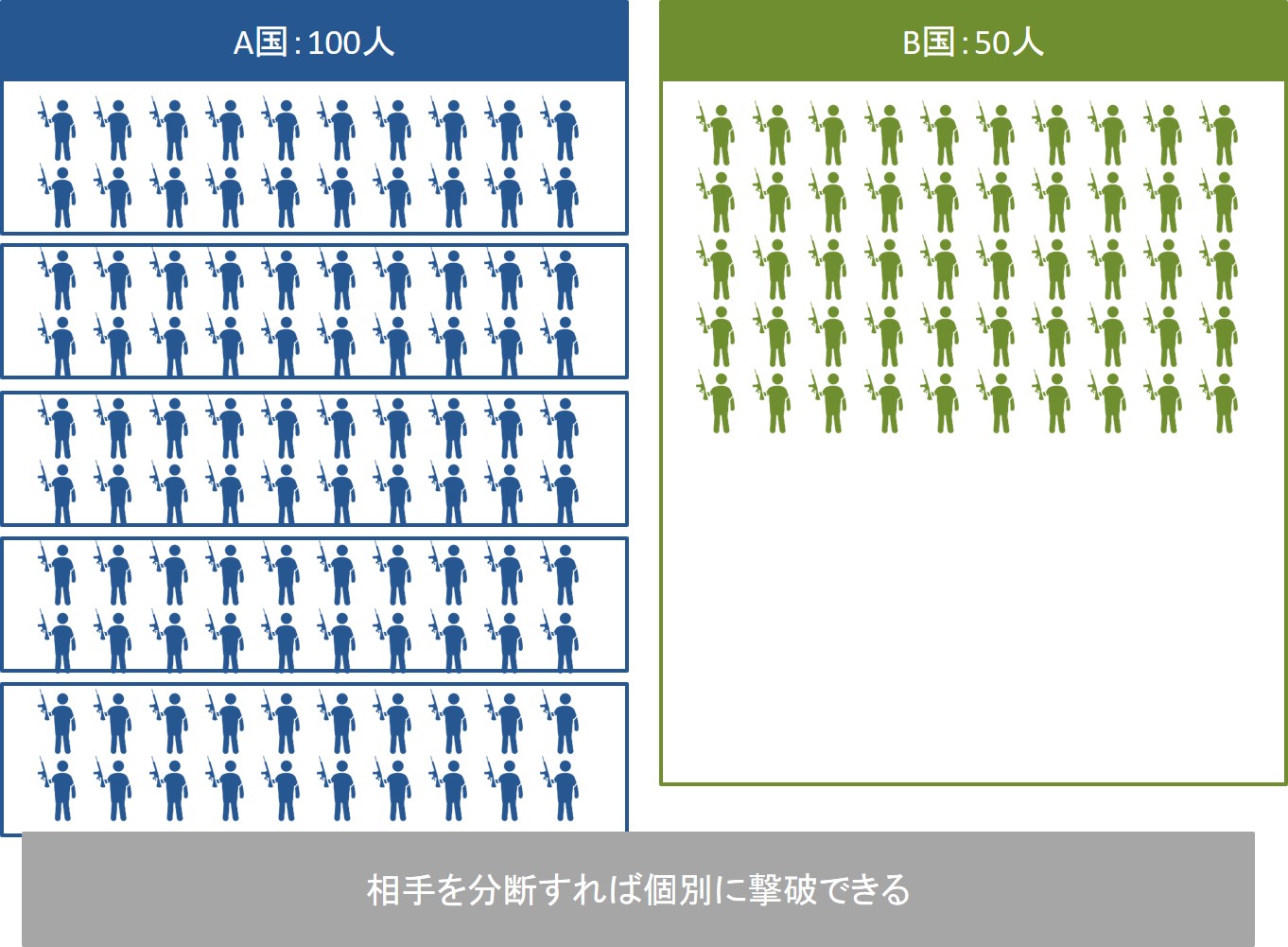
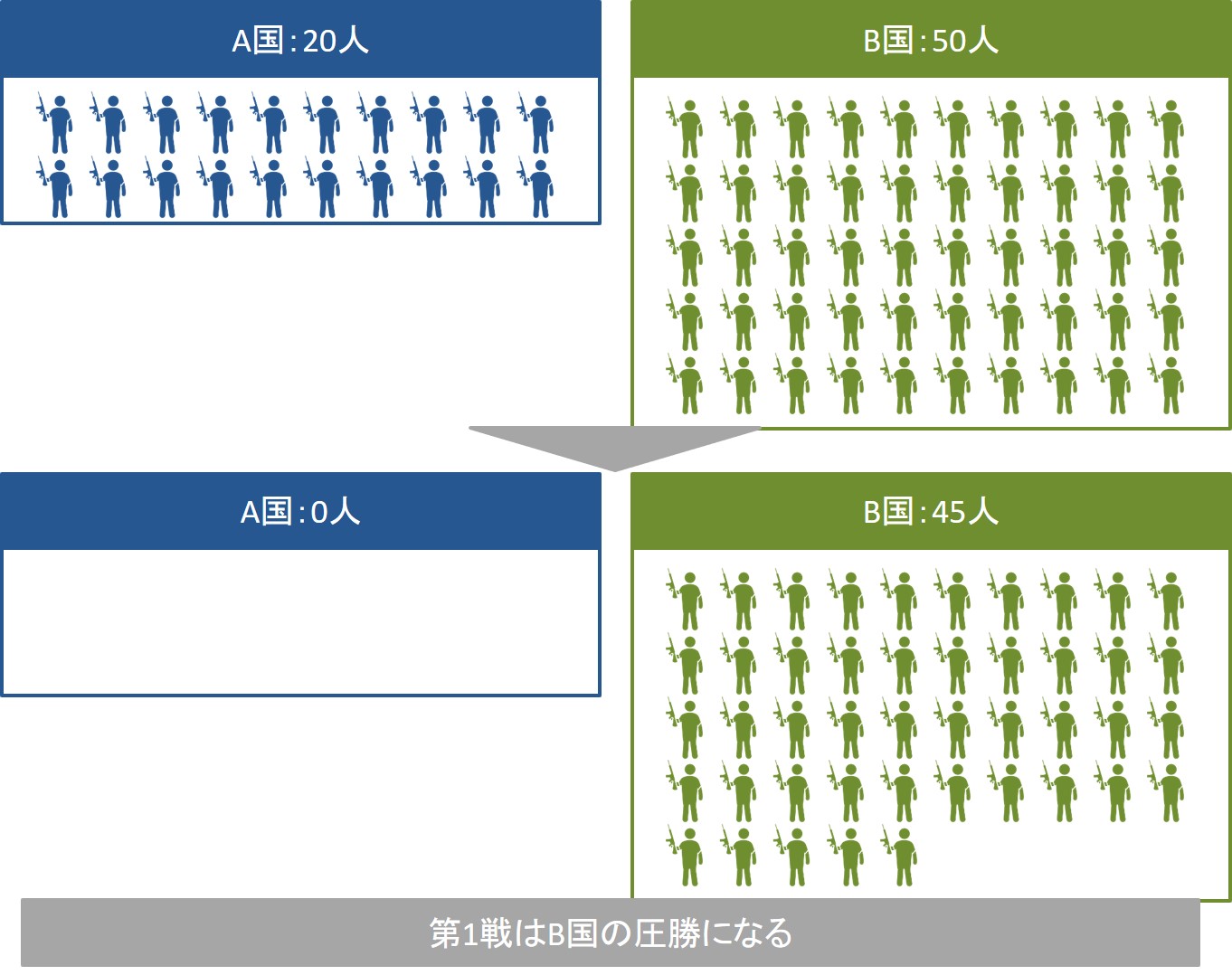
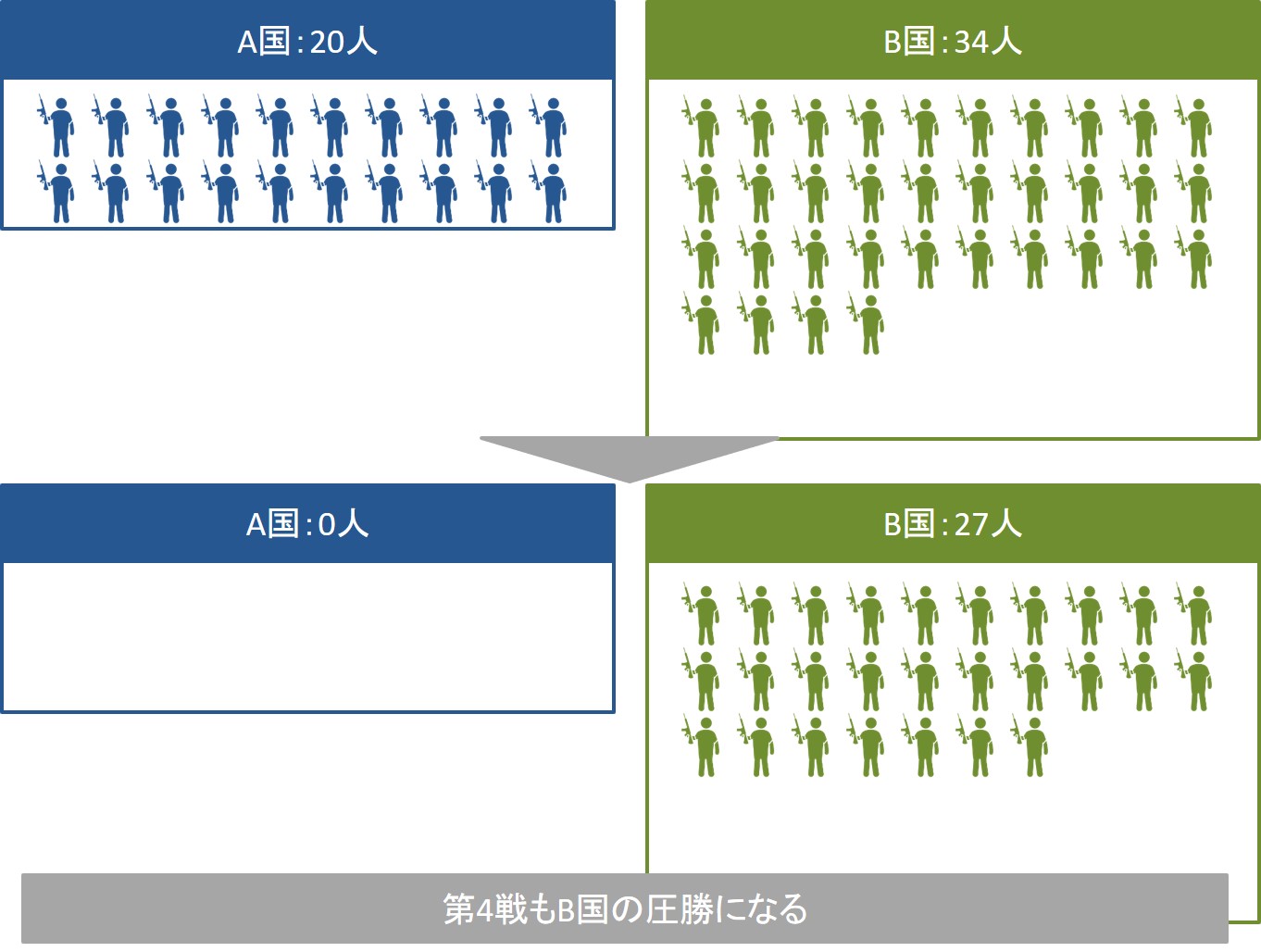
こうなると、B国は50人の兵士を使って、20人を順番に撃破すればよいことになります。
最初にB国の50人の兵士と、A国の20人の兵士が戦うと、「兵力数の2乗の差は常に一定である」というランチェスターの第二法則によると、戦闘後のB国の兵力数は45人になります。(計算結果の小数点以下は切り捨てています)
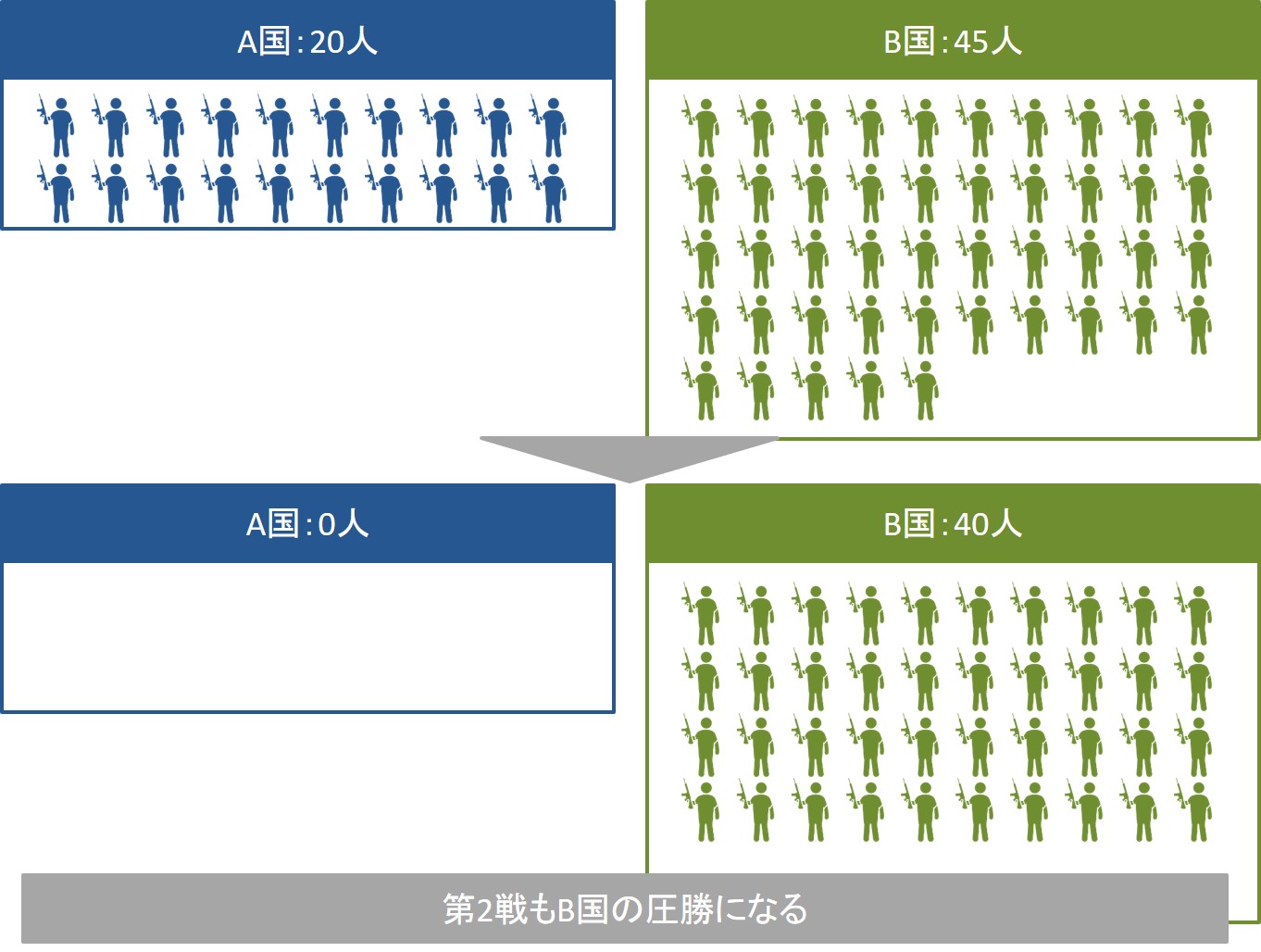
次にB国の45人の兵士と、A国の20人の兵士が戦うと、戦闘後のB国の兵力数は40人になります。
これを繰り返していくと、以下のようになり、最終的にはB国の兵力数は18人まで減りますが、A国を撃破できることがわかります。
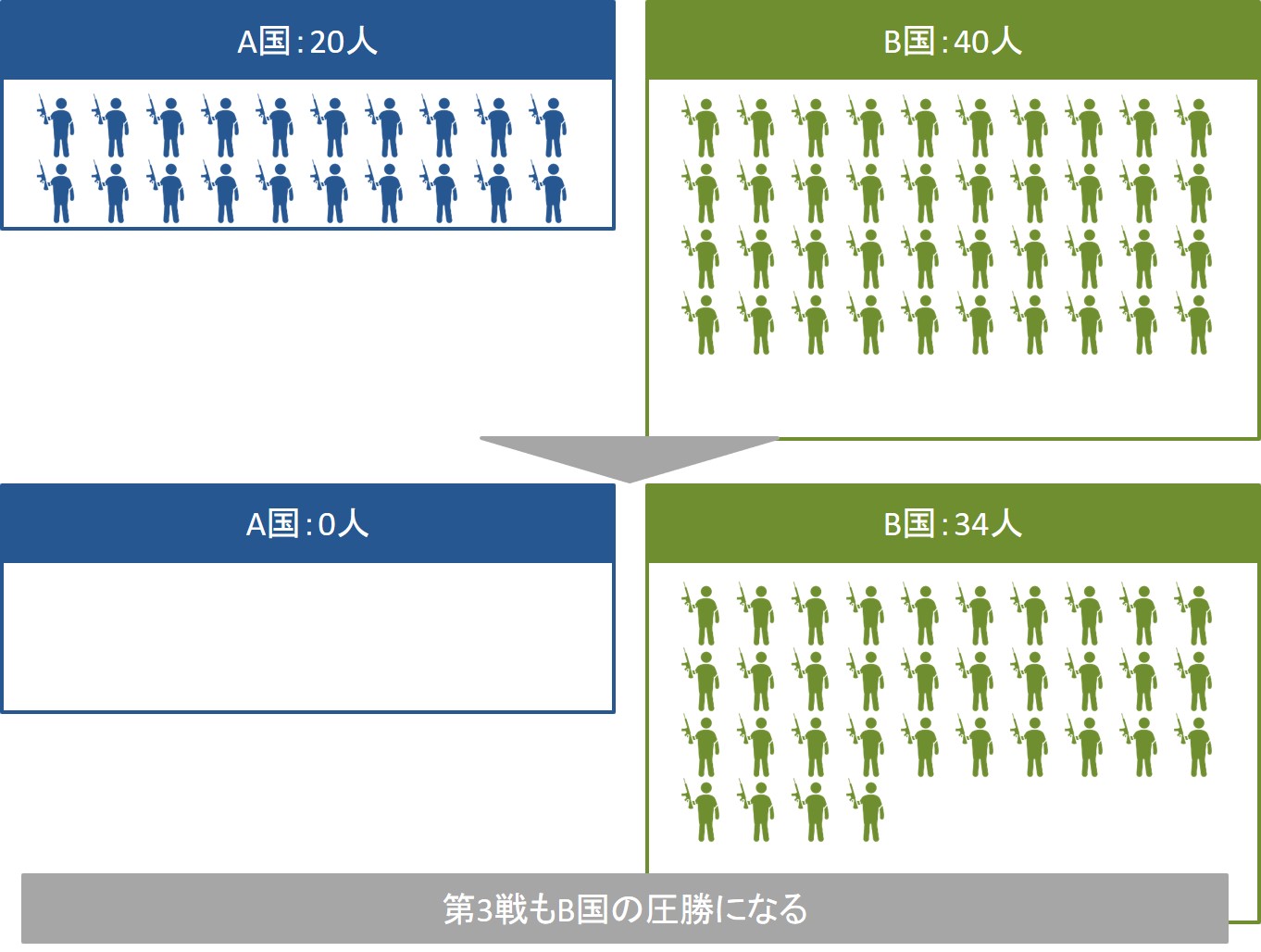
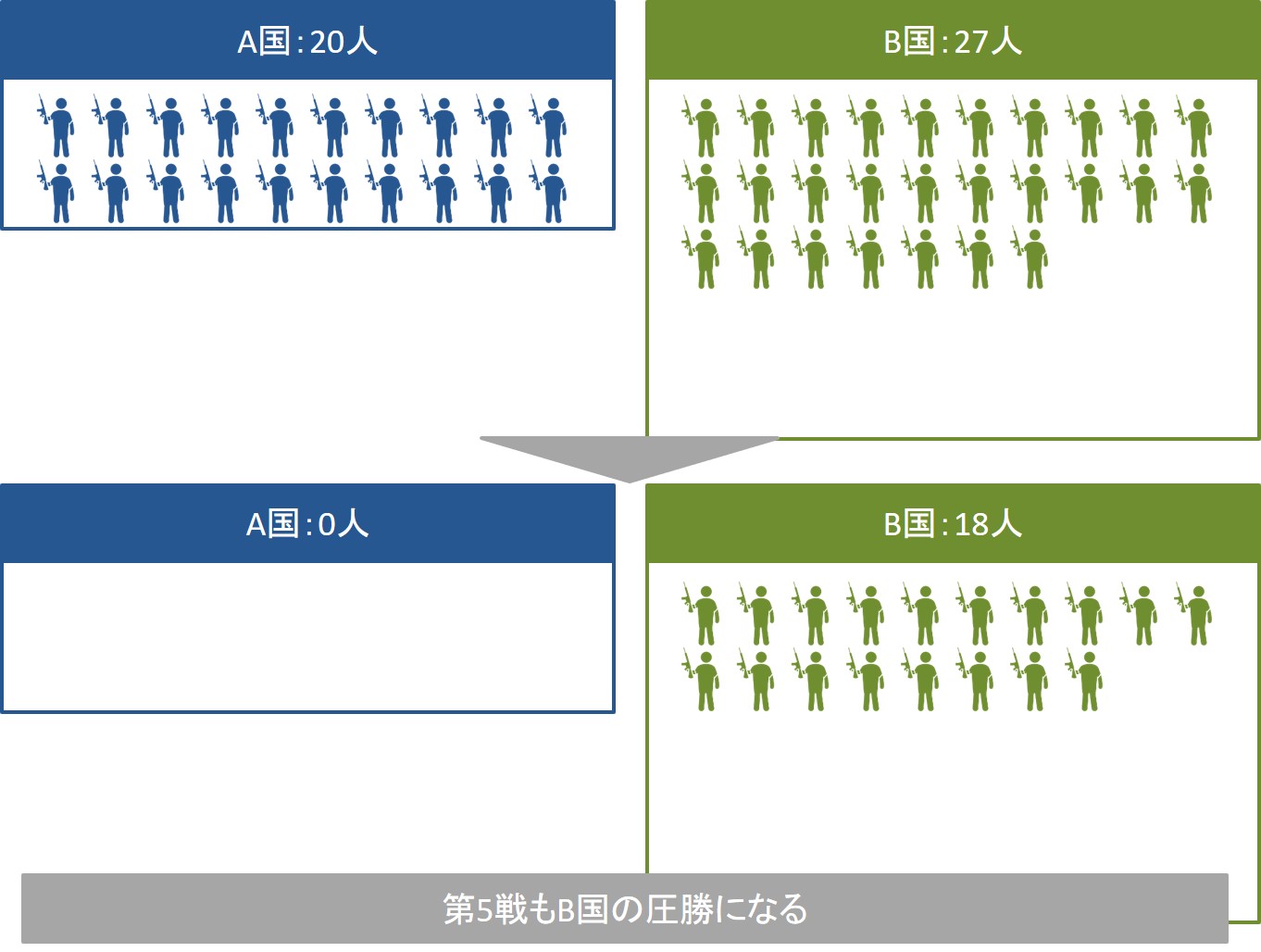
このことから、相手が巨大な兵力を持っている場合は、相手を分断して一点突破の戦いを何度も繰り返す形にすることで、兵力数が少なくても勝てることがわかります。
ランチェスター戦略の応用例
ランチェスター戦略の応用例を2つ紹介します。
弱者の活用例:ダイソン
ランチェスター戦略を弱者の側で活用した例として、「吸引力が変わらない唯一の掃除機」というキャッチコピーで掃除機業界に進出したダイソンがあります。
ダイソンが進出した当時の掃除機業界には、各国で古くから活躍していた家電メーカーが多数ありました。
その中で、ダイソンは掃除機のユーザーが持っていた潜在的な不満・困りごとである「吸引力」に目をつけて、吸引力の訴求に集中することで、「ハイブランドな掃除機と言えばダイソン」と認知されるまでのメーカーになりました。
やがて、扇風機やドライヤーなど、掃除機で培ってきたモーター技術を活用して、それぞれの分野で一点突破を目指そうとしています。
強者の活用例:パナソニック
ランチェスター戦略は、弱者の側だけでなく強者の側でも活用できます。
強者の側は、弱者が強者に勝つための逆、すなわち以下のことをすればよいのです。
- 局地戦を避ける
- 一点突破に備える
- 戦力を分断しないようにする
かつてのパナソニックは、競合が新しい商品を出すとすかさず追随して、販売網や広告宣伝力などの圧倒的な物量をベースに競合を寄せ付けないようにしていました。
これはランチェスター戦略でいうと、上記3つのことを避けていると同時に、武器性能での劣勢を速やかに解消することで、常に競合に対して優位性を保つための戦略でもあります。
パナソニック以外でも、多くのトップ企業が、競合に対して武器性能を同等にし、上記の隙きを見せないようにしています。
まとめ
以上、ランチェスター戦略の解説でした。
- ランチェスター戦略とは、戦闘をする双方が同じ武器を持っているとするなら、勝敗は兵力数によって決まることを示したランチェスターの法則をベースにした戦略のことである。
- ランチェスターの第一法則では、戦闘力=武器性能×兵力数と定義される。言い換えると、兵力数の差は常に一定であることを示す。
- ランチェスターの第二法則では、戦闘力=武器性能×兵力数の2乗と定義される。言い換えると、兵力数の2乗の差は常に一定であることを示す。
- ランチェスター戦略を活用すると、局地戦に持ち込む、一点突破をする、相手を分断するという3つの方向性が弱者にとって有効な戦略となる。(逆に、強者はこれらを防ぐ必要がある。