【四分割表】人に騙されないための方法【因果関係を客観的に分析しよう】

「ついつい人に騙されてしまう。」

「声の大きい人の言い分を信じてしまう。」

ビジネスの場面で、このような感覚を持ってしまうことも少なくないと思います。

今回は、人に騙されたり、迷信をついつい信じてしまうがちな人に向けて、四分割表を使った騙されないための方法を解説しています。

四分割表は、ロジカルシンキングを鍛えるためにも有用なフレームワークです。

騙されないために考えること

騙されないことを考える前に、騙されるとはどういう状態かを考えてみましょう。

よくあるのが、以下のような話です。

売る側は言葉巧みに買えば儲かると説明して、買う側がその話を信じて買ったのに、結果として儲からない。

こうなると買った側は、「私は騙された」と感じます。

このように、騙される状態というのは「AをしたらBが起きる」という因果関係を信じ込まされた上で、AをしてもBが起きない状態のことを指すのです。

上記のように騙される状態がわかるようになると、騙されないようにするための方法はその逆だとわかります。

つまり、

ということが、はっきりすれば騙されることも少なくなるのです。

しかし、相手から言葉巧みに説得されているときに、冷静になって考えることは簡単ではありません。

特に、相手に騙されるときは、「この人が言うのだから。。。」という感情的な部分も作用してきます。

そうしたときに、冷静に考えるためのツールが四分割表なのです。

四分割表とは

四分割表とは、心理学者のトーマス・ギロビッチによって考案されたもので、相関関係の確からしさを検証するためのものです。（ギロビッチの著書「人間この信じやすきもの―迷信・誤信はどうして生まれるか」で詳しく解説されています）

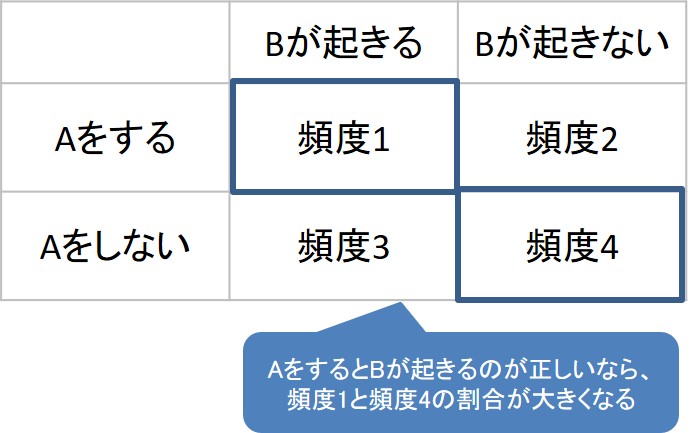
AをするとBが起きるという事象に対して、四分割表を作ると次のようになります。

	Bが起きる	Bが起きない
Aをする	頻度1	頻度2
Aをしない	頻度3	頻度4

四分割表では、AをするとBが起きることを検証するためには、Aをする場合にBが起きる頻度1とBが起きない頻度2、Aをしない場合にBが起きる頻度3と、Bが起きない頻度4を検証できます。

もし、AをするとBが起きるのであれば、次のような結果を得られるはずです。

四分割表の使い方

四分割表を使った例を2つの本から引用します。

1つめは、「独学大全――絶対に「学ぶこと」をあきらめたくない人のための55の技法」に慶されている雨乞いの事例です。

今どき、雨乞いをすることで雨が降ると信じている人はいないでしょうが、以下のように四分割表を作ってみれば、より客観的に判断をできるようになります。

	降雨あり	降雨なし
雨乞いをする	頻度1	頻度2
雨乞いをしない	頻度3	頻度4

実際に、頻度1と頻度4が割合として大きくならないことは明白でしょう。

2つめは、「なぜ疑似科学が社会を動かすのか ヒトはあやしげな理論に騙されたがる」に掲載されているお守りの事例です。

お守りの場合も、その効果があるかどうかを四分割表を作って検証することで明らかにすることができます。

	良いことが起きる	悪いことが起きる
お守りを持っている	頻度1	頻度2
お守りを持っていない	頻度3	頻度4

先ほどの「これを買えば、必ず儲かりますよ」という儲け話にも同じように適用することができます。

ここでは商材Xとして、以下のように四分割表を作ります。

	儲かる	儲からない
商材Xを買う	頻度1	頻度2
商材Xを買わない	頻度3	頻度4

言葉巧みに説得されている状態で、頻度1～4を検証する時間はないかもしれませんが、四分割表を作って考えてみると少なくとも頻度1以外の可能性にも目を向けることができます。

たとえば、以下のように考えることができます。

確証バイアスに注意

四分割表で客観的に考える際に注意すべきことに、確証バイアスがあります。

確証バイアスとは、自分の思い込みをサポートする情報を重視して、そうでない情報を軽視することです。

たとえば、転職をするかしないかという議論のときに、転職経験者が「転職をするべき」と言って、転職未経験者が「転職はやめたほうがよい」と言う場合は、確証バイアスに陥っている可能性があります。

なぜなら、転職経験者、未経験者がそれぞれ自分の経験を正当化できるように、自分のとった選択をサポートする情報を重視するからです。

これを四分割表で見ると、以下のような構図になります。

	良いことが起こる	悪いことが起こる
転職をする	転職経験者が強調する	転職未経験者が強調する
転職をしない	転職未経験者が強調する	転職経験者が強調する

一般的には転職するしないによって、良いことが起きるかどうかはケースバイケースだと思いますが、確証バイアスが働くと客観的な判断の妨げになってしまうのです。

商材Xの例でも確証バイアスによる認知の歪みが起きる可能性があります。

たとえば、商材Xを紹介する人が尊敬する人であったり、商材Xを買うことを前提にして判断材料を集めると四分割表の中で偏った情報ばかりを集めるようになってしまいます。

	儲かる	儲からない
商材Xを買う	自分が買う商材に間違いはないと考えて、儲かっている事例ばかり見てしまう	買った人の努力が足りなかったと考える
商材Xを買わない	この可能性は考えない	ー

まとめ

以上、四分割表を使った人に騙されない方法についてでした。