このブログでこれまで紹介してきた投資意思決定は、基本的に単一の意思決定でした。
しかし、現実社会ではある意思決定を待つと、状況が変わって予測される収益の確度が上がるという場面もあります。その概念を表したのがリアルオプションです。
この記事では、そのリアルオプションについて解説していきます。
リアルオプションとは
投資においては、投資額の半分を最初に投資して、1年後の成長が順調なら継続投資を行い、1年後の成長が鈍ければ事業からの撤退(あるいは投資規模縮小)するという判断をすることがあります。
リアルオプションとは、こうした継続投資か撤退(あるいは縮小)かを投資初期の段階から織り込んで、DCF法による投資収益計算を行う手法です。リアルオプションでは、将来の収益に及ぼす事象が起こる可能性までを含めた投資判断を行っていきます。
リアルオプションを考えるのに役立つツールのひとつとしてディシジョンツリーがあります。
デシジョンツリー
あるプロジェクトに3000万円投資したときのリターンの現在価値が30%の確率で10000万円、30%の確率で5000万円、40%の確率で1000万円になるとします。
これをツリーで表すと、次のようになります。
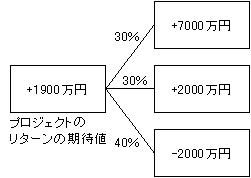
さて、ここでプロジェクトへの投資を1年待てば投資へのリターンが確実に分かるとします。このとき、1000万円のリターンしかないということがわかれば、投資はしないことになるのでツリーは次のようになります。(割引率を5%として、投資額とリターンの現在価値を換算しなおしています。)

つまり、1年待って将来のリターンが確実に分かることには、2572-1900=672万円の価値があることになります。これは待つというオプションに対する価値に他なりません。
そうなると、たとえば投資のリターンが1年で確実にわかるような市場調査にかけるお金は672万円が最大値であることがわかります。逆に、それ以上お金をかけるなら、数字上はすぐに投資したほうがよいことになります。(ただし、絶対に-1500万円以上の損失は許されないという状況であれば、調査費が672万円~1500万円ならお金をかけてでも市場調査をすべきという判断になります。
デシジョンツリーの事例
ある商品を開発するために技術Xと技術Yという2つの新技術の開発が必要だと仮定します。
前提条件
技術X:開発費500万円、成功確率75%
技術Y:開発費350万円、成功確率85%
この2つの技術の開発に成功した場合、他社に真似されるまで1280万円の販売利益を得られるとします。
技術Xと技術Yを同時開発する場合
まず技術XとYを同時開発した場合のツリーは以下のようになります。

この場合、期待損益は以下のようになります。
期待販売利益 = 1280万円 * 63.75% = 816万円
開発費 = 500万円+350万円 = 850万円
期待損益 = 期待利益 ー 開発費 = 816万円ー850万円 = -34万円
技術Xを最初に開発する場合
次に技術Xを最初に開発して、技術Yを後から開発するケースを考えると以下のようになります。

この場合、期待損益は以下のようになります。
期待販売利益 = 1280万円 * 75% * 85% = 816万円
開発費 = 500万円 * 25% + (500万円 + 350万円)*75% = 762.5万円
期待損益 = 期待利益 ー 開発費 = 816万円ー762.5万円 = 53.5万円
ここでのポイントは、技術Xの開発に失敗したら技術Yを開発しないという選択肢があることです。このオプションを持つことによって必要となる開発費を減らすことができるのです。
技術Yを最初に開発する場合
最後に技術Yを最初に開発して、技術Xを後から開発するケースを考えると以下のようになります。
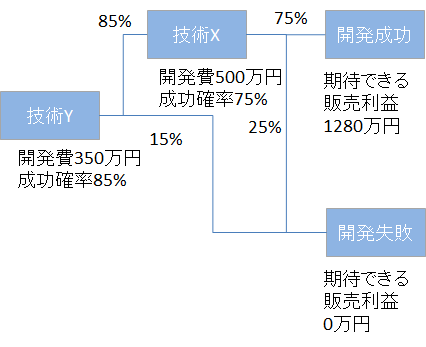
この場合、期待損益は以下のようになります。
期待販売利益 = 1280万円 * 85% * 75% = 816万円
開発費 = 350万円 * 15% + (350万円 + 500万円)*85% = 775万円
期待損益 = 期待利益 ー 開発費 = 816万円ー775万円 = 41万円
上の例と同様に、技術Yの開発に失敗したら、技術Xを開発しないという選択肢があることによって必要となる開発費を減らすことができるのです。
ただし、失敗確率が低くかつ開発費の少ない技術Yを先に開発して、失敗確率・開発費ともに高い技術Xを後から開発するので、開発費の総額は技術Xを先に開発するケースよりも大きくなってしまいます。
まとめ
このように、リアルオプション、ディジョンツリーを使うことで、選択肢に時間軸を入れてオプション検討できるようになります。
実際、不確実性を伴う選択肢がある場合は、上記のように条件を満たしてから次のステップに移るようにすることでリスクを軽減できるのです。
経営だけでなく日常の意思決定にも使える考え方ですので、みなさんも活用してみてはいかがでしょうか。

