回帰分析とは【単回帰分析と重回帰分析の解説】エクセルでの求め方

ビジネスにおいて、ある変数と別の変数の関係を分析する方法として回帰分析があります。

回帰分析を使うことで、過去のデータを元に、未来を予測できるようになります。

この記事では、2つの回帰分析、単回帰分析と、重回帰分析について解説していきます。

関係性を数字を使って明らかにすることは、ロジカルシンキングの能力を鍛えることにもつながります。

回帰分析とは

回帰分析とは、ある原因に対し、結果となる数字がどのような関係性で示されるかを調べる際に用います。

たとえば、原因となる値をXとして、結果となる値をYとすると、次のような式で表すことができます。

この中で、ビジネスの実務上最もよく使われる1次式（Y ＝ a・X + b）による回帰分析の例を見ていきます。

ここで、Xのことを説明変数、Yのことを目的変数と呼びます。

回帰分析は、たとえば来店者数と売上の関係や、気温の売上の関係などを過去のデータを使って、関係性を明らかにする場合に使われます。

単回帰分析とは

回帰分析には2つの種類があります。

そのうちの1つが、単回帰分析です。

単回帰分析の目的は、目的変数Yが1つの説明変数Xによってどの程度変化するか、またはどの程度信頼できるかを予測し明らかにすることです。

単回帰分析の結果を式で表すと以下のようになります。

単回帰分析をする場合、データ数は最低でも10個は欲しいところです。

10個以下でも計算式を導けますが、目的変数と説明変数の関係を信頼度高く分析するためには、10個がひとつの目安になります。

エクセルを使った単回帰分析の方法

単回帰分析は、エクセルを使うと簡単にできます。

たとえば、以下のような説明変数Xと目的変数Yの関係性があったとしましょう。

X	10	12	3	14	4	10	6	11	9	11
Y	16	17	3	26	7	18	10	15	15	14

この2つ変数を散布図を使ってグラフ化します。

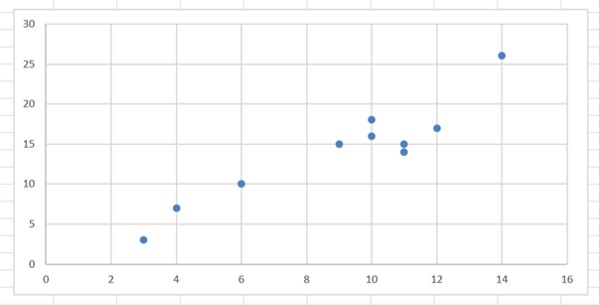
次に散布図のプロットを右クリックして、、「近似曲線を追加」を押します。

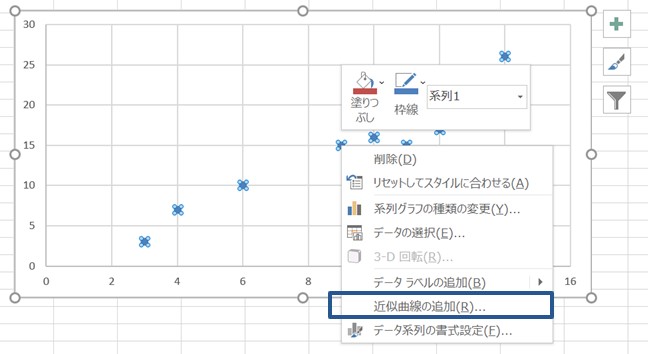
近似曲線のオプションを「線形近似」のままにして、「グラフに数式を表示する」と、「グラフにR-2乗値を表示する」にチェックを入れます。

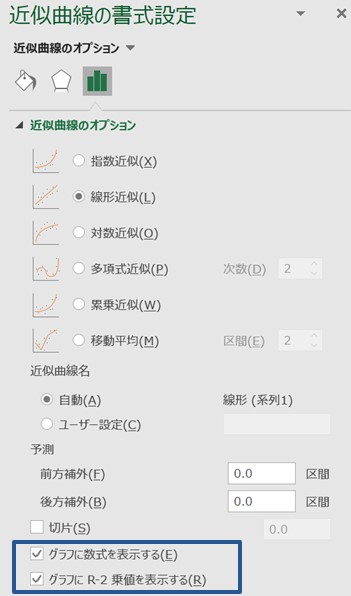
すると、このような近似線が出来上がります。

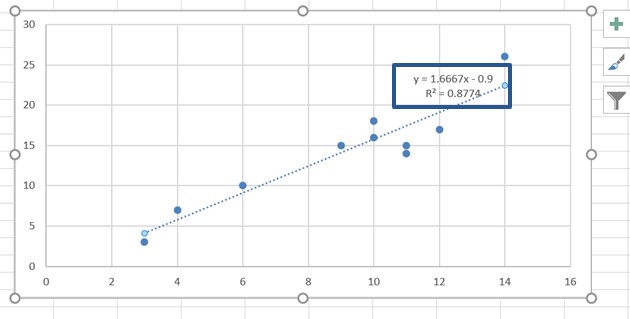
これで、単回帰分析は完了です。

つまり、先ほどの説明変数Xと目的変数Yの関係性は、以下の式で表されることになります。

この式を使えば、今後Xがどのような値になったときに、Yがどのような値になるかを予測できるわけです。

回帰式におけるR²の意味

単回帰分析で導いた近似線にR²値が表示されていますが、

R²値とは決定係数と呼ばれるもので、推定された回帰式の確からしさを表します。

R²値は0から1までの値をとり、1に近いほど回帰式が確からしいことを示し、説明変数が目的変数を説明しているといえます。

逆に0に近ければ、回帰式の確からしさが低いことを示します。

簡単にいうと、R²値が1なら100%、0.5なら50%、0なら0%の確からしさになっていると考えればよいでしょう。

先ほどのグラフだと、R²値は0.8774なので、2つの変数の関係は9割方は描いた回帰式で説明がつくということになります。

一般的には、R²値が0.5～0.8なら回帰式が成立する可能性が高いとされていて、0.8以上であれば成立する可能性がかなり高いことを示します。

なお、ここで出てくるR²値は相関係数の2乗になります。

関連記事：相関係数とは【意味・目安・エクセルでの求め方】

重回帰分析とは

もう1つの回帰分析が、重回帰分析です。

単回帰分析とは、2つ以上の説明変数と、1つの目的変数の関係性を示すための分析です。

単回帰分析が1つの目的変数を1つの説明変数で予測したのに対して、重回帰分析は1つの目的変数を複数の説明変数で予測します。

身長のみから体重を予測するのが単回帰分析だとすると、身長と腹囲の2つの説明変数から体重を予測するのは重回帰分析になります。

重回帰分析の結果を式で表すと以下のようになります。

エクセルを使った重回帰分析の方法

エクセルを使えば、重回帰分析も簡単にできてしまいます。

たとえば、以下のように列Aに目的変数Y、列Bと列Cに説明変数X1、X2があるとします。

	Y	X1	X2
	A	B	C
1	10	16	10
2	12	17	11
3	3	3	2
4	14	26	15
5	4	7	5
6	10	18	9
7	6	10	6
8	11	15	13
9	9	15	7
10	11	14	14

重回帰分析をするためのコマンドは、エクセルのデフォルト状態にはないので、コマンドをツールバーに出すための作業必要です。

まず「ファイル」から「オプション」を選択します。

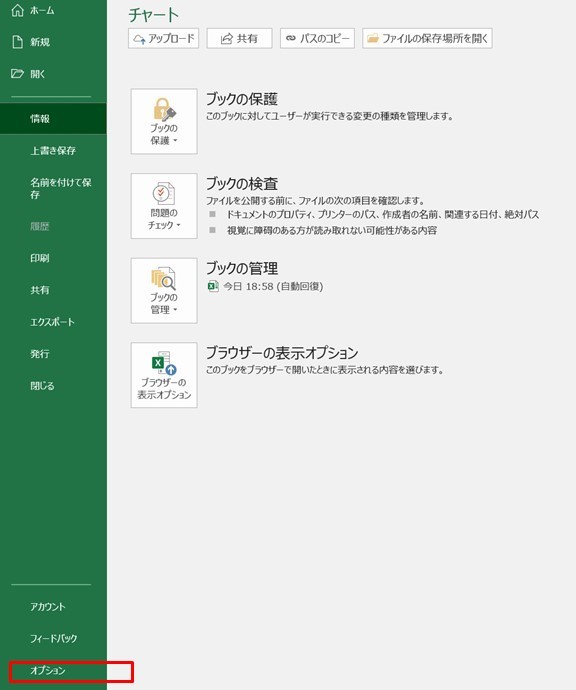
「オプション」の中にある「アドイン」から「分析ツール」を選んで、「設定」ボタンを押します。

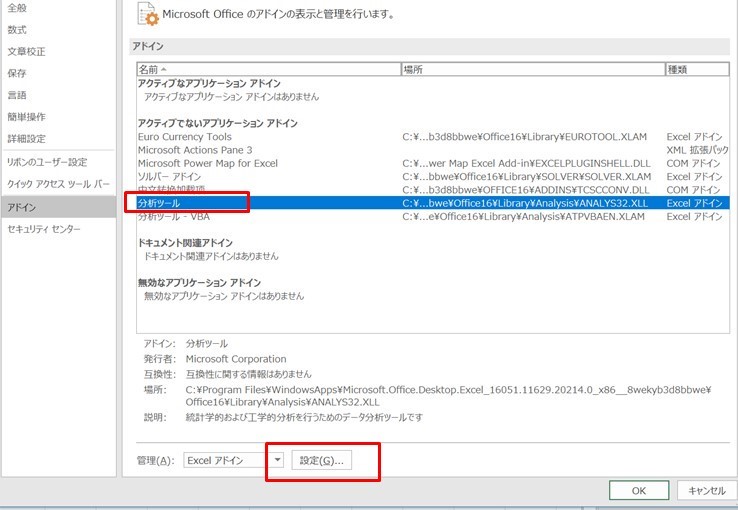
「分析ツール」を選んで「OK」を押します。

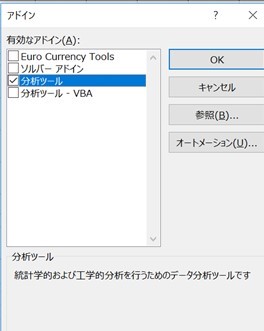
これでエクセルのメニューの「データ」の一番右側に「分析ツール」が入ります。

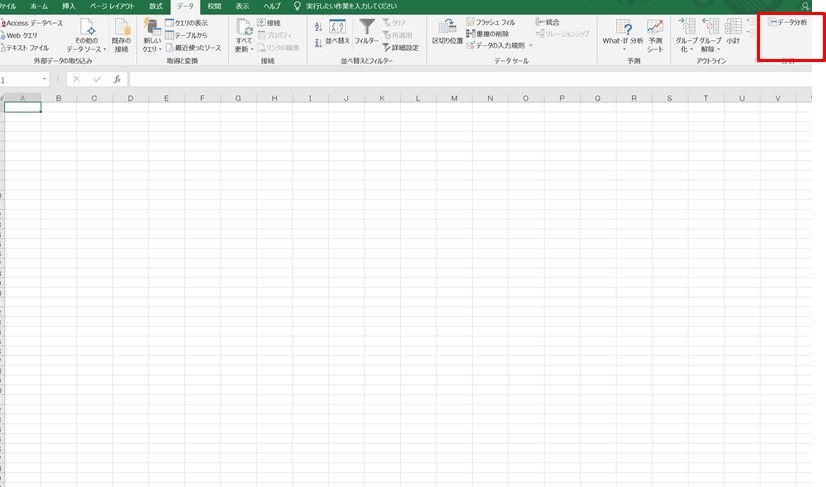
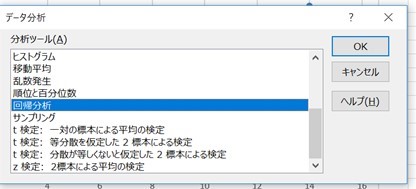
次に「分析ツール」の中から「データ分析」を押して、「回帰分析」を選択し、「OK」のボタンを押します。

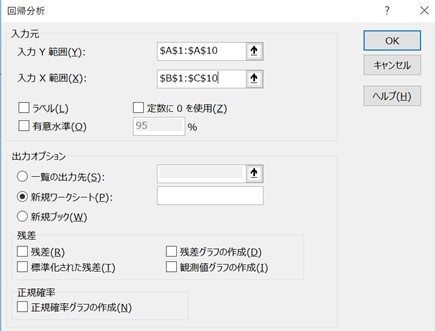
ここで、先ほどのデータを以下のように選択します。

YがA1からA10、XがB1からC10の範囲です。

ここで「OK」ボタンを押すと、別シートに以下のような数字が出てきます。

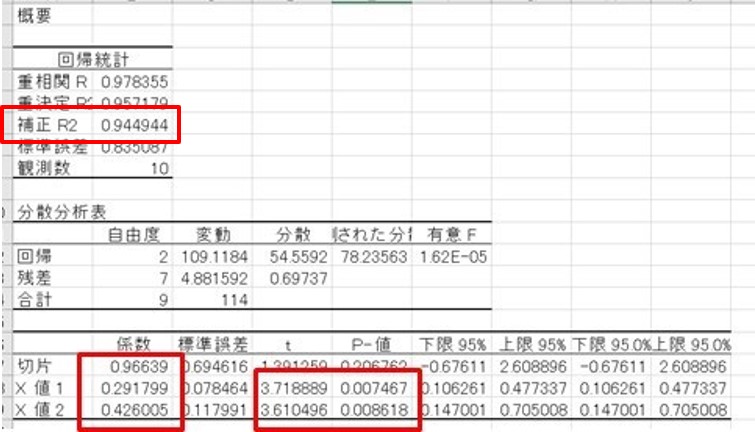
ここから、係数のところに出てきた値を使って、重回帰分析の結果を次のような表します。

※小数点第三位を四捨五入しています。

重回帰分析で注目すべき3つの値

重回帰分析では、上の図で赤で囲んだ係数以外の3つの値に注意する必要があります。

補正R²値

補正R²値とは、単回帰分析におけるR²値と同じ意味を表します。

つまり、重回帰分析から導いた数式が、どのくらいの確率で正しいのかを示しています。

補正R²値の上に、重相関Rや重決定R²などがありますが、細かいことを説明すると長くなるので、ここでは補正R²値が重要だと覚えておきましょう。

ｔ値

t値が大きい変数は、目的変数Yとの関係性がより強いことを示します。

t値が2を超えているかどうかが、説明変数X1とX2を採用できるかどうかの判断材料になります。

事例の場合、両方とも2を超えているので、X1、X2を説明変数として採用できると判断できます。

P値

P値が、0.05よりも大きいときは、その説明変数を採用しないほうがよいとされています。

先ほどの例では、両方とも0.05を下回っているので、X1、X2を説明変数として採用できると判断できます。

なお、t値とP値は、相関の強い説明変数を2つ以上用いると、不採用の可能性が高くなります。

たとえば、家賃を目的変数Yとして、説明変数X1を「駅からの距離」と説明変数X2を「地価」とします。

もし、説明変数X1の「駅からの距離」とX2の「地価」同士に強い相関があると、X1とX2のどちらかの変数は、t値またはP値の基準外になってしまうでしょう。

回帰分析の注意点

回帰分析は、現象の傾向を表すのに非常に有効なツールですが、回帰分析を使うと、それらしい近似曲線をいくらでも導くことができてしまいます。

そうした特徴を持つ回帰分析からのアクションをより有効なものにするために、2つの注意点があります。

数字の背後にある前提条件を観察する

回帰分析で分析できるのは、過去のデータの関係性だけです。

もし、その関係性がある前提条件のもとでだけ成り立っているとしたら、前提条件が将来変化したときに回帰分析をした関係性とは異なる結果が出るかもしれません。

回帰分析をする際には、その関係性を生み出している前提条件を明らかにして、その前提条件が未来にも適用可能なのかを注意深く考える必要があります。

関係性から大きく外れた値の扱いに注意する

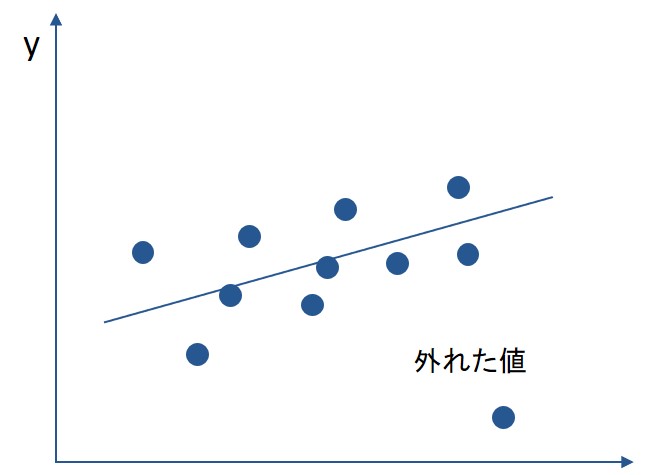
2つの値の関係をグラフにすると、明らかに他の関係性から大きく外れたデータが出てくる場合があります。

回帰分析をする際には、外れたデータを含んだまま回帰分析をするのか、除外するのか判断する必要があります。

もし、外れた値が、特定の前提条件で発生したものであれば、外れた値を除いて回帰分析をしなおす必要があります。

一方で、外れた値には、ビジネス上の大きなヒントが隠されている場合もあるので、個別に掘り下げてみることも必要です。

回帰分析はどのようなときに使うのか？

ビジネスにおいては、原因と結果の因果関係を明らかにするために回帰分析が用いられます。

たとえば、以下のような分析をしたいときに、回帰分析は有効です。

過去のデータにもとづいて、これらのことを分析できれば、未来予測に使えるようになります。

たとえば、過去のデータから気温とアイスクリームの売れ行きを分析できれば、翌日の天気予報をもとにして、翌日のアイスクリームの売れ行きを予測できます。

回帰分析は、このように未来予測の正確性を高めるために使われているのです。

まとめ

以上、回帰分析の解説でした。